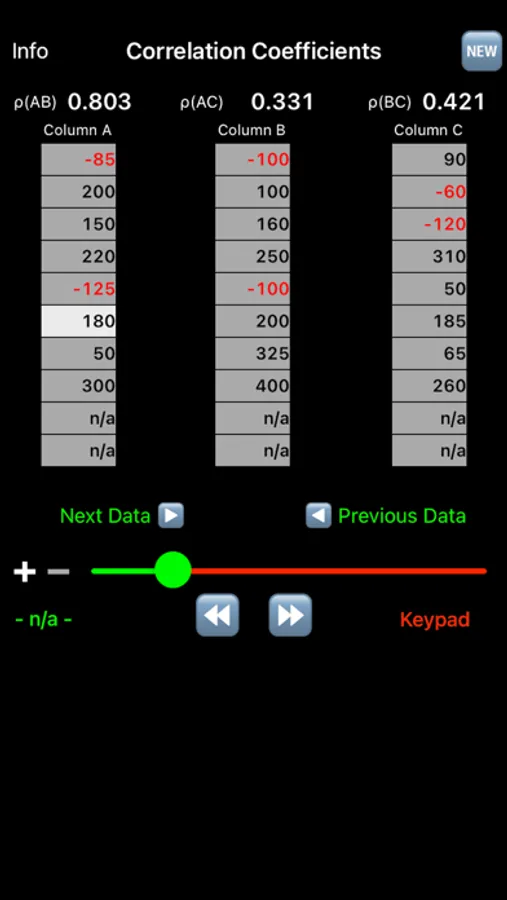
The correlation coefficient (commonly noted by the Greek letter rho, ρ) measures the degree to which two sets of numbers are related. The correlation coefficient can range from -1.000 to +1.000 with a 0 indicating that there is no relation between the two sets.
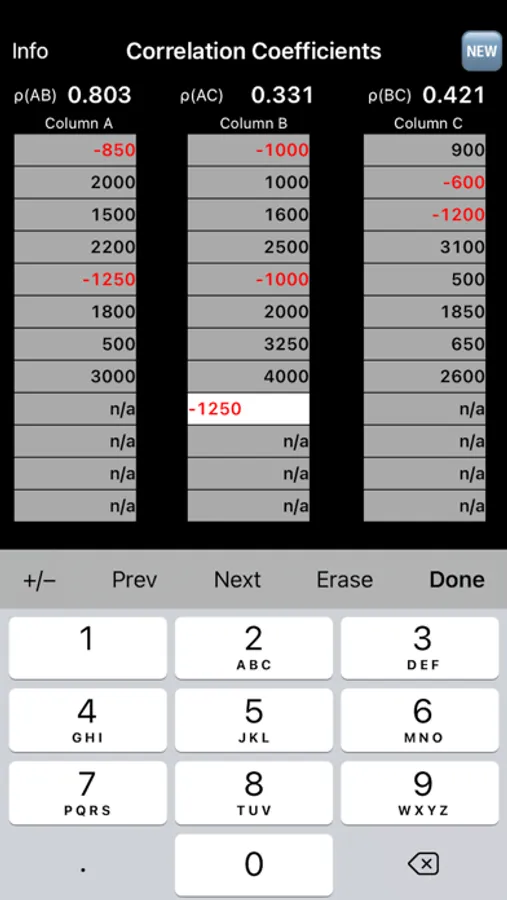
A 'slider' data entry option allows rapid creation of numerical data. Additionally, you may use the 'keypad' data entry option to expand the numerical range beyond plus or minus 1,000.
In this application, you may relate two or three sets of numbers and the correlations between the sets are shown as ρ(AB), ρ(AC), and ρ(BC), where the letters A, B, and C represent the columns.
There must be at least 3 pairs of numbers in any 2 rows for the correlation coefficient to be computed. Zero is a number but 'n/a' is not. If, for example, Column A has 5 rows of numbers and the 6th row is 'n/a' and Column B has 4 rows of numbers and the 5th row is 'n/a', the correlation coefficient, ρ(AB), will be computed for the first 4 pairs of numbers.
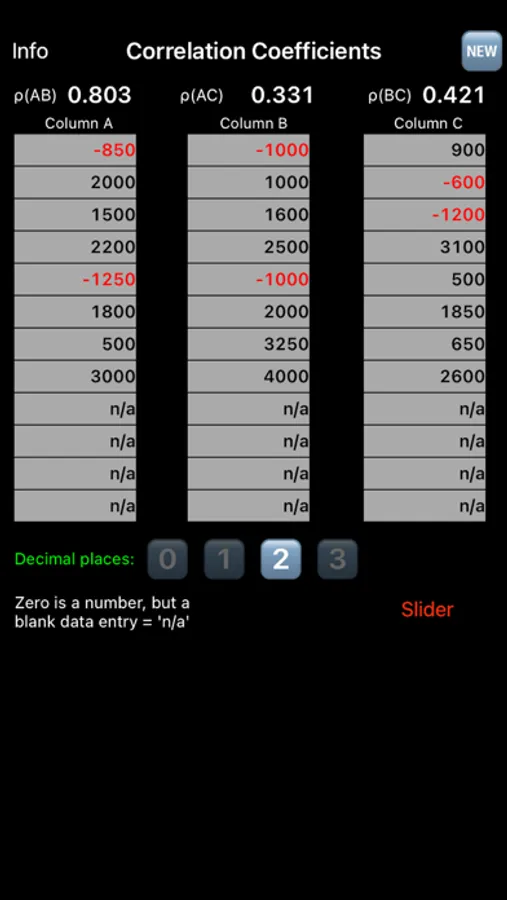
A 'slider' data entry option allows rapid creation of numerical data. Additionally, you may use the 'keypad' data entry option to expand the numerical range beyond plus or minus 1,000.
In this application, you may relate two or three sets of numbers and the correlations between the sets are shown as ρ(AB), ρ(AC), and ρ(BC), where the letters A, B, and C represent the columns.
There must be at least 3 pairs of numbers in any 2 rows for the correlation coefficient to be computed. Zero is a number but 'n/a' is not. If, for example, Column A has 5 rows of numbers and the 6th row is 'n/a' and Column B has 4 rows of numbers and the 5th row is 'n/a', the correlation coefficient, ρ(AB), will be computed for the first 4 pairs of numbers.
Show More
